Minggu, 07 April 2013
Misteri Bilangan 0
RATUSAN tahun yang lalu, manusia hanya mengenal 9 lambang bilangan yakni 1, 2, 3, 4, 5, 6, 7, 8, dan 9. Kemudian, datang angka 0, sehingga jumlah lambang bilangan menjadi 10 buah. Tidak diketahui siapa pencipta bilangan 0, bukti sejarah hanya memperlihatkan bahwa bilangan 0 ditemukan pertama kali dalam zaman Mesir kuno. Waktu itu bilangan nol hanya sebagai lambang.Dalam zaman modern, angka nol digunakan tidak saja sebagai lambang, tetapi juga sebagai bilangan yang turut serta dalam operasi matematika. Kini, penggunaan bilangan nol telah menyusup jauh ke dalam sendi kehidupan manusia. Sistem berhitung tidak mungkin lagi mengabaikan kehadiran bilangan nol, sekalipun bilangan nol itu membuat kekacauan logika. Mari kita lihat.
Nol, penyebab komputer macet
Pelajaran tentang bilangan nol, dari sejak zaman dahulu sampai sekarang selalu menimbulkan kebingungan bagi para pelajar dan mahasiswa, bahkan masyarakat pengguna. Mengapa? Bukankah bilangan nol itu mewakili sesuatu yang tidak ada dan yang tidak ada itu ada, yakni nol. Siapa yang tidak bingung? Tiap kali bilangan nol muncul dalam pelajaran Matematika selalu ada ide yang aneh. Seperti ide jika sesuatu yang ada dikalikan dengan 0 maka menjadi tidak ada.
Mungkinkah 5*0 menjadi tidak ada? (* adalah perkalian). Ide ini membuat orang frustrasi.
Apakah nol ahli sulap?
Lebih parah lagi-tentu menambah bingung-mengapa 5+0=5 dan 5*0=5 juga? Memang demikian aturannya, karena nol dalam perkalian merupakan bilangan identitas yang sama dengan 1. Jadi 5*0=5*1. Tetapi, benar juga bahwa 5*0=0. Waw.
Bagaimana dengan 5o=1, tetapi 50o=1 juga? Ya, sudahlah. Aturan lain tentang nol yang juga misterius adalah bahwa suatu bilangan jika dibagi nol tidak didefinisikan. Maksudnya, bilangan berapa pun yang tidak bisa dibagi dengan nol.
Komputer yang canggih bagaimana pun akan mati mendadak jika tiba-tiba bertemu dengan pembagi angka nol. Komputer memang diperintahkan berhenti berpikir jika bertemu sang divisor nol.
Bilangan nol: tunawisma
Bilangan disusun berdasarkan hierarki menurut satu garis lurus . Pada titik awal adalah bilangan nol, kemudian bilangan 1, 2, dan seterusnya. Bilangan yang lebih besar di sebelah kanan dan bilangan yang lebih kecil di sebelah kiri. Semakin jauh ke kanan akan semakin besar bilangan itu. Berdasarkan derajat hierarki (dan birokrasi bilangan), seseorang jika berjalan dari titik 0 terus-menerus menuju angka yang lebih besar ke kanan akan sampai pada bilangan yang tidak terhingga. Tetapi, mungkin juga orang itu sampai pada titik 0 kembali. Bukankah dunia ini bulat?
Mungkinkah? Bukankah Columbus mengatakan bahwa kalau ia berlayar terus-menerus ia akan sampai kembali ke Eropa?
Lain lagi. Jika seseorang berangkat dari nol, ia tidak mungkin sampai ke bilangan 4 tanpa melewati terlebih dahulu bilangan 1, 2, dan 3. Tetapi, yang lebih aneh adalah pertanyaan mungkinkan seseorang bisa berangkat dari titik nol? Jelas tidak bisa, karena bukankah titik nol sesuatu titik yang tidak ada? Aneh dan sulit dipercaya? Mari kita lihat lebih jauh.
Perhatikan garis bilangan , di antara dua bilangan atau antara dua buah titik terdapat sebuah ruas. Setiap bilangan mempunyai sebuah ruas. Jika ruas ini dipotong-potong kemudian titik lingkaran hitam dipindahkan ke tengah-tengah ruas, ternyata bilangan 0 tidak mempunyai ruas. Jadi, bilangan nol berada di awang-awang.
Bilangan nol tidak mempunyai tempat tinggal alias tunawisma. Itulah sebabnya, mengapa bilangan nol harus menempel pada bilangan lain, misalnya, pada angka 1 membentuk bilangan 10, 100, 109, 10.403 dan sebagainya. Jadi, seseorang tidak pernah bisa berangkat dari angka nol menuju angka 4. Kita harus berangkat dari angka 1.
Mudah, tetapi salah
Guru meminta Ani menggambarkan sebuah garis geometrik dari persamaan 3x+7y = 25. Ani berpikir bahwa untuk
mendapatkan garis itu diperlukan dua buah titik dari ujung ke ujung. Tetapi, setelah berhitung-hitung, ternyata cuma ada satu titik yang dilewati garis itu, yakni titik A(6, 1), untuk x=6 dan y=1 (Gambar 2). Sehingga Ani tidak bisa membuat garis itu.
Sang guru mengingatkan supaya menggunakan bilangan nol. Ya, itulah jalan keluarnya. Pertama, berikan y=0 diperoleh x=(25-0)/3=8 (dibulatkan), merupakan titik pertama, B(8,0). Selanjutnya berikan x=0 diperoleh y=(25-3.0)/7=4 (dibulatkan), merupakan titik kedua C(0,4). Garis BC, adalah garis yang dicari. Namun, betapa kecewanya sang guru, karena garis itu tidak melalui titik A. Jadi, garis BC itu salah.
Ani membela diri bahwa kesalahan itu sangat kecil dan bisa diabaikan. Guru menyatakan bahwa bukan kecil besarnya kesalahan, tetapi manakah yang benar? Bukankah garis BC itu dapat dibuat melalui titik A? Kata guru, gunakan bilangan nol dengan cara yang benar. Bagaimana kita harus membantu Ani membuat garis yang benar itu? Mudah, kata konsultan Matematika. Mula-mula nilai 25 dalam 3x+7y harus diganti dengan hasil perkalian 3 dan 7 sehingga diperoleh 3x+7y=21.
Selanjutnya, dalam persamaan yang baru, berikan y=0 diperoleh x=21/3=7 (tanpa pembulatan) itulah titik pertama P(6,1).
Kemudian berikan nilai x=0 diperoleh y=21/7 = 3 (tanpa pembulatan), itulah titik kedua Q(0, 3). Garis PQ adalah garis yang sejajar dengan garis yang dicari, yakni 3x+7y=25. Melalui titik A tarik garis sejajar dengan PQ diperoleh garis P1Q1. Nah, begitulah. Sang murid telah menemukan garis yang benar berkat bantuan bilangan nol.
Akan tetapi, sang guru masih sangat kecewa karena sebenarnya tidak ada satu garis pun yang benar. Bukankah dalam persamaan 3×1+7×2=25 hanya ada satu titik penyelesaian yakni titik A, yang berarti persamaan 3×1+7×2 itu hanya berbentuk sebuah titik? Bahkan pada persamaan 3×1+7×2=21 tidak ada sebuah titik pun yang berada dalam garis PQ.
Oleh karena itu, garis PQ dalam sistem bilangan bulat, sebenarnya tidak ada. Aneh, bilangan nol telah menipu kita.
Begitulah kenyataannya, sebuah persamaan tidak selalu berbentuk sebuah garis.
Bergerak, tetapi diam
Bilangan tidak hanya terdiri atas bilangan bulat, tetapi juga ada bilangan desimal antara lain dari 0,1; 0,01; 0,001; dan seterusnya sekuat-kuat kita bisa menyebutnya sampai sedemikian kecilnya. Karena sangat kecil tidak bisa lagi disebut atau tidak terhingga dan pada akhirnya dianggap nol saja. Tetapi, ide ini ternyata sempat membingungkan karena jika bilangan tidak terhingga kecilnya dianggap nol maka berarti nol adalah bilangan terkecil? Padahal, nol mewakili sesuatu yang tidak ada? Waw. Begitulah.
Berdasarkan konsep bilangan desimal dan kontinu, maka garis bilangan pada Gambar 1a tidak sesederhana itu karena antara dua bilangan selalu ada bilangan ke tiga. Jika seseorang melompat dari bilangan 1 ke bilangan 2, tetapi dengan syarat harus melompati terlebih dahulu ke bilangan desimal yang terdekat, bisakah? Berapakah bilangan desimal terdekat sebelum sampai ke bilangan 2? Bisa saja angka 1/2. Tetapi, anda tidak boleh melompati ke angka 1/2 karena masih ada bilangan yang lebih kecil, yakni 1/4. Seterusnya selalu ada bilangan yang lebih dekat… yakni 0,1 lalu ada 0,01, 0,001, …, 0,000001. demikian seterusnya, sehingga pada akhirnya bilangan yang paling dekat dengan angka 1 adalah bilangan yang demikian kecilnya sehingga dianggap saja nol. Karena bilangan terdekat adalah nol alias tidak ada, maka Anda tidak pernah bisa melompat ke bilangan 2?
(Yusmichad Yusdja,Staf peneliti pada Pusat Penelitian dan Pengembangan Sosial dan ekonomi Pertanian IPB)
sumber : roabaca.com
Cara Menjumlahkan Pecahan Campuran
Saat pertama kali menerima murid belajar di tempat les, biasanya saya akan ‘mengujinya’ pengetahuan dasar yang sudah mereka miliki. Bagaimana cara mereka mengerjakan soal-soal perkalian termasuk hafalan perkalian dasar mereka, cara menjumlahkan, konsep pecahan yang mereka pahami dan lain-lain. Ini saya lakukan untuk mendapatkan gambaran sejauh mana pemahaman dan kemampuan matematika masing-masing anak.
Khusus menyangkut pecahan pecahan campuran, saya sering sekali menemukan hal ‘salah kaprah’ seperti ini,
4 ¼ + 2 3/5 = 17/4 + 13/5
= 85 /20 + 52 /20
= 137/20
= 6 17/20
Secara matematis, sebenarnya cara di atas tidak sepenuhnya salah. Hanya terlalu ‘ribet’ karena melibatkan perhitungan yang banyak dan tidak efisien.
Murid yang datang dengan kasus seperti ini biasanya akan saya bimbing menghitung penjumlahan bilangan campuran dengan memberi contoh sehari-hari misalnya potongan kue. Saya minta dia membayangkan potongan kue sebesar 4 ¼ dan 2 3/5 dan meminta mereka menggabungkannya. Saya lalu membimbing mereka menarik kesimpulan bahwa saat menggabungkan kue tersebut bukan berarti kue tersebut harus saya potong dulu menjadi dua puluh bagian. Bukankah bisa dilakukan dengan menjumlahkan bagian kue yang utuh? Setelah itu menjumlahkan bagian kue yang sudah dipotong hingga menghasilkan perhitungan sebagai berikut :
4 ¼ + 2 3/5 = 4 + 2 + 1/4 + 3/5
= 6 + 5 /20 + 12 /20
= 6 17/20
Cara ini jauh lebih mudah dan praktis bukan ?
http://pintarmatematika.wordpress.com
Yuk… Bermain Perkalian dengan Bilangan 11!
Perkalian dengan bilangan 11 sering saya jadikan permainan unik di sela-sela waktu pengajaran. Siswa biasanya akan terperangah dan kagum dengan keajaiban perkalian bilangan 11.
Berikut keajaiban perkalian dengan bilangan 11:
1. Bilangan 1 angka jika dikalikan dengan bilangan 11 akan menghasilkan bilangan berulang angka tersebut. Contoh 2 x 11 = 22.
2. Bilangan 2 angka jika dikalikan dengan bilangan 11 akan menghasilkan bilangan 3 angka dengan susunan angka pertama dari hasil perkalian sama dengan angka asal, angka ketiga hasil perkalian sama dengan angka kedua asal dan angka kedua hasil perkalian adalah hasil penjumlahan angka pertama dan kedua. Contoh : 23 x 11 = 253.
3. Hal kedua diatas juga berlaku bagi bilangan lebih dari 2 angka. Contoh : 1234 x 11 = 13574
dimana angka 1 pada hasil sama dengan angka 1 bilangan asal.
angka 3 pada hasil adalah penjumlahan 1+2 (angka pertama dan kedua) pada bilangan asal.
angka 5 pada hasil adalah penjumlahan 2+3 (angka kedua dan ketiga) pada bilangan asal.
angka 7 pada hasil adalah penjumlahan 3+4 (angka ketiga dan keempat) pada bilangan asal.
angka terakhir 4 pada hasil sama dengan angka terakhir bilangan asal.
Bagaimana mengerjakan soal 19 x 11?
Cobalah mengutak atik dengan berpedoman pada langkah-langkah yang diajarkan di atas. Satu catatan penting adalah ingat proses ‘menyimpan’ jika hasil penjumlahan kedua angka sama atau lebih dari 10!
Selamat bersenang-senang
http://pintarmatematika.wordpress.com/
Sulap Matematika : Menebak Bilangan Awal
Ini jenis sulap yang lain karena kali ini pesulap harus bisa menebak bilangan awal yang di’simpan’ penonton. Berikut langkah-langkah permainannya :
1. Minta anak sebagai penonton untuk memikirkan sebuah bilangan dan merahasiakannya.
2. Minta dia mengalikannya dengan 2.
3. Hasilnya kalikan 5.
4. Tanyakan hasil akhir yang diperolehnya.
5. Berapapun hasil akhirnya, kita dapat menebaknya dengan mudah. Cukup dengan cara membuang angka terakhir pada bilangan yang disebutkannya. Agar terlihat lebih seru, usahakan seakan Anda sebelumnya nampak serius berpikir.
Catatan :
Sesuaikan bilangan yang dipilih dengan tingkat kemampuan anak tersebut. Anak berusia 7-8 tahun sebaiknya memilih bilangan 1 angka saja. Ini memudahkan sekaligus dapat melatihnya menghafal perkalian dasar. Sesuatu yang sulitkan kalau meminta anak langsung menghafal perkalian?
Untuk anak yang lebih besar sebaiknya menggunakan bilangan yang lebih kompleks. Selain menghitung dengan bantuan ‘kotretan’ mereka pun dapat sekaligus berlatih mental aritmatika. Ingat berlatih akan membuat mereka makin cepat dan tepat dalam berhitung.
Contoh langkah pada sulap matematika ini :
1. 76
2. 76 x 2 = 152
3. 152 x 5 = 760
4. Buang angka terakhir 0 dan kita berhasil menebak 76!
Hehe…betul! Rahasianya tentu saja di langkah kedua dan ketiga. Mengalikan dengan 2 dan 5 sama artinya dengan mengalikan 10! Aha… ini bisa Anda gunakan untuk mengenalkan sifat perkalian dengan bilangan kelipatan 10, 100 dan seterusnya.
Cobalah membuat soal dengan memodifikasi bilangan 100 sebagai perkalian 4 dan 25. Misalnya.
1. Simpan bilangan 23.
2. 23 x 4 = 92.
3. 92 x 25 = 2300.
4. Tos…betul! Hilangkan 2 angka terakhir
Selamat bersenang-senang…..
sumber gambar : orbit-digital.com
http://pintarmatematika.wordpress.com
KPK Matematika
Bukan ini bukan KPK yang artinya Komisi Pemberantasan Korupsi. KPK yang dibahas di sini adalah Kelipatan Persekutuan Terkecil. Kemampuan siswa mengerjakan soal KPK matematika merupakan salah satu syarat wajib yang harus dikuasai siswa.
Sebenarnya apa sih KPK itu? KPK adalah Kelipatan Persekutuan Terkecil. Dari definisinya saja terlihat bahwa siswa harus menguasai masalah kelipatan untuk menguasai tuntas materi ini. Mengajarkan kelipatan dapat dilakukan dengan pendekatan dua cara. Cara pertama yaitu konsep bilangan loncat yang telah dipelajari dari sejak kelas 1 SD. Sedangkan cara kedua dapat dilakukan dengan mengingatkannya pada konsep perkalian dasar.
Contoh soal kelipatan: Sebutkan kelipatan dari 2!
Jawab : Kelipatan 2= 2, 4, 6, 8 ,10, dan seterusnya.
Pengertian persekutuan menunjukkan bahwa ada lebih dari satu pihak yang terlibat. Karena itu kelipatan persekutuan melibatkan dua bilangan atau lebih.
Contoh soal kelipatan persekutuan: Sebutkan kelipatan persekutuan dari 2 dan 3!
Jawab : Kelipatan 2= 2, 4, 6, 8 ,10, 12, 14, 16. 18 dan seterusnya.
Kelipatan 3 = 3, 6, 9, 12, 15, 18, 21 dan seterusnya.
Maka kelipatan persekutuannya adalah 6, 12, 18 dan seterusnya.
Penjelasan sampai di sini biasanya sudah mampu mengantarkan siswa mengambil kesimpulan bahwa kpk (kelipatan persekutuan terkecil) dari 2 dan 3 adalah 6.
Contoh tahapan soal KPK matematika lainnya:
Tentukan KPK dari 3 dan 5!
Kelipatan dari 3 = 3, 6, 9, 12, 15, 18, 21, 24 dan seterusnya.
Kelipatan dari 5 = 5, 10, 15, 20, 25 dan seterusnya.
Kelipatan persekutuan 3 dan 5 = 15, 30, 45 dan seterusnya
KPK dari 3 dan 5 adalah 15.
Contoh soal KPK matematika lainnya:
Tentukan KPK dari 10 dan 12!
Kelipatan dari 10 = 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130 dan seterusnya.
Kelipatan dari 12= 12, 24, 36, 48, 60, 72, dan seterusnya.
Kelipatan persekutuan dari 10 dan 12= 60, 120 dan seterusnya.
KPK dari 10 dan 12 = 60.
Soal KPK matematika biasanya juga disajikan dalam bentuk soal cerita seperti soal berikut: Amir dan Badu les berenang. Mereka mulai les pada tanggal 1 tapi jadwalnya berbeda. Amir memilih jadwal les setiap dua hari. Adapun Badu memilih jadwal les setiap tiga hari. Kapan pertemuan mereka yang kedua?
Mereka pertama kali berjumpa tanggal 1. Untuk menentukan waktu pertemuan mereka yang kedua dapat dilakukan dengan mencari KPK 2 dan 3. KPK 2 dan 3 = 6 (lihat penentuan KPK di atas). Berarti mereka akan berjumpa lagi 6 hari kemudian atau pada tanggal 7.
http://pintarmatematika.wordpress.com
Sistem Bilangan Romawi
Walau terkesan ‘mudah’, sering sekali saya menjumpai siswa atau bahkan orang dewasa yang mengalami kesulitan membaca dan menuliskan bilangan romawi. Padahal sistem ini sering digunakan misalnya pada penulisan ilmiah, bab dan halaman buku, dan lain-lain.
I bernilai 1.
V bernilai 5.
X bernilai 10.
L bernilai 50.
C bernilai 100.
D bernilai 500.
M bernilai 1000.
Berikut tata cara penggunaannya:
1. Pengulangan huruf hanya berlaku pada 1, 10, 100 dan seterusnya. Misalnya 200 ditulis sebagai CC dan tidak bisa 100 ditulis sebagai LL.
2. Pengulangan pada poin 1 di atas hanya berlaku maksimal tiga kali. Misalnya XXX berarti 30 tapi tak ada XXXX.
3. Lambang yang di depan bermakna pengurang lambang di belakangnya. Contoh IX berarti (10-1=9) dan XL berarti (50-10=40).
4. Poin 3 berlaku pada lambang yang berdekatan dan tak berlaku jika loncat. Contoh 99 tidak bisa ditulis dalam bentuk IC (100-1) karena letak I dan C tidak ‘berdekatan’.
5. Jika lambang yang lebih besar berada di depan lambang lebih kecil bermakna tambah, misalnya nilai 110 dilambangkan dengan CX.
6. Untuk bilangan yang lebih besar atau sama dengan 5000 maka terjadi pengulangan lambang di atas dengan penambahan garis di atas huruf. Garis tersebut berarti ‘dikalikan’ 1000. Jadi lambang V dibaca (5×1000=5000) demikian seterusnya.
Contoh:
MDCXXI dibaca 1621 (M bernilai 1000, DC bernilai 500+100 atau 600, XX bernilai 20 dan I bernilai 1).
MCXCVIII dibaca 1198 (M bernilai 1000, C bernilai 100, XC bernilai 100-10 atau 90 dan VIII bernilai 5+3 atau 8).
MMLXXIV dibaca 2074 (MM bernilai 2000, tak ada nilai ratusan, LXX bernilai 70 dan IV artinya 5-1 = 4)
Mudah bukan?
Sekarang bilangan berapakah ini MCDLXXXIX?
http://pintarmatematika.wordpress.com
Cara Mudah Menentukan Bilangan Prima
Beberapa anak kesulitan menentukan bilangan prima. Berikut cara mudah mencari bilangan prima dengan bantuan tabel perkalian.
Langkah pengerjaannya adalah sebagai berikut :
2. Minta anak mencoret semua kelipatan 3 kecuali 3.
3. Minta anak mencoret semua kelipatan 5 kecuali 5.
4. Minta anak mencoret semua kelipatan 7 kecuali 7.
5. Manakah bilangan yang tidak tercoret? Itulah bilangan prima!
Definisi bilangan prima adalah bilangan yang hanya memiliki dua faktor saja yaitu 1 dan dirinya sendiri. Sedangkan pengertian faktor lebih jelas dengan memberikan contoh sebagai berikut.
2 x 5 = 10 karena itu dikatakan 2 dan 5 adalah faktor dari 10. Jelas bukan?
Nah kembali ke definisi bilangan prima. Bilangan 2 adalah bilangan prima karena hanya memiliki faktor 1 dan 2. Bilangan 4 bukan bilangan prima karena memiliki faktor 1,2 dan 4.
Cara mencari bilangan prima dengan menggunakan bantuan tabel perkalian seperti cara di atas dikenal sebagai cara Saringan Erasthothenes.
http://pintarmatematika.wordpress.com
Mahir Perkalian dengan Bilangan Kelipatan 11
Sudah tahu kan trik melakukan perkalian dengan bilangan 11? Kalau bilangan satu angka dikalikan 11 sih pasti mudah, iya kan? Contohnya 2 x 11 tentu saja 22. Nah tapi bagaimana kalau 4521 x 11.
Mudah, jawabannya pasti 49731. Kalau belum bisa menghitung lancar soal perkalian tadi, silakan klik ini untuk mempelajari lebih lanjut
Nah sekarang jurus mahir perkaliannya ditambah lagi nih. Kali ini perkalian dengan bilangan kelipatan 11, misalnya 22, 33 dan seterusnya.
Begini aturan dasar perkalian ini:
Contoh : 7 x 33
1. Kalikan dengan bilangan kelipatan 10 yang lebih kecil dari 33. Ingat untuk menggunakan trik perkalian dengan bilangan yang menggunakan angka 0. Jadi 7 x 30 = 210.
2. Tambahkan hasil tadi dengan 10% nya. Jadi 210 + 21 = 231.
Contoh-contoh lainnya : (sebelum mencoba menghitung, sebaiknya tidak melihat jawabannya dulu ya
1. 8 x 55 = …
berarti 8 x 50 = 400. Lalu 400 + 40 = 440.
2. 9 x 22 = …
berarti 9 x 20 = 180. Lalu 180 + 18 = 198.
3. 17 x 33 = …
berarti 17 x 30 = 510. Lalu 510 + 51 = 561.
Mudah bukan?
http://pintarmatematika.wordpress.com
Cara Mudah Menentukan Akar Pangkat 2
Murid biasanya lebih mudah memahami konsep bilangan berpangkat
dibanding akar pangkat suatu bilangan. Mereka pun lebih mudah
mengerjakan soal-soal perpangkatan dibanding soal menentukan akar
pangkat suatu bilangan. Sebagai catatan, murid SD biasanya akan diminta
untuk menentukan akar pangkat 2 atau akar pangkat 3.
Cara yang lazim digunakan biasanya dengan cara yang dinamakan mencabut akar. *jadi kebayang mencabut akar singkong. Susahkan. Ini candaanku sama murid
 Dengan
alasan mencari yang praktis dan memudahkan, jarang sekali saya
mengajarkan cara seperti itu. Saya cenderung memilih cara mudah dan
efisien. Pertimbangannya tak mungkin soal-soal menentukan akar pangkat 2
akan menghasilkan bentuk bilangan desimal. Pasti itu!
Dengan
alasan mencari yang praktis dan memudahkan, jarang sekali saya
mengajarkan cara seperti itu. Saya cenderung memilih cara mudah dan
efisien. Pertimbangannya tak mungkin soal-soal menentukan akar pangkat 2
akan menghasilkan bentuk bilangan desimal. Pasti itu!
Cara yang saya ajarkan pada murid untuk menentukan akar pangkat 2 adalah sebagai berikut :
1. Saya minta murid menentukan angka satuan (ingat angka satuan, berarti angka yang paling akhir ya pada bilangan 1 sampai 9 yang dipangkatkan 2.
pada bilangan 1 sampai 9 yang dipangkatkan 2.
Langkah ini akan menghasilkan daftar seperti ini :
1^2 = 1 (simbol 1^2 dibaca 1 kuadrat ya, atau 1 pangkat 2 atau 1×1
2^2 = 4
3^2 = 9
4^2 = 6 (ingat satuannya saja ya…)
5^2 = 5
6^2 = 6
7^2 = 9
8^2 = 4
9^2 = 1
(Perhatikan ada hasil yang memberikan nilai satuan yang sama. Hati-hati!)
2. Langkah berikutnya adalah menentukan perpangkatan bilangan puluhan.
10^2 = 100
20^2 = 400
30^2 = 900
40^2 = 1600 dan seterusnya.
Penerapan di soal menentukan akar pangkat 2 dari sebuah bilangan :
a. Tentukan akar pangkat 2 dari 289.
Jika melihat dari langkah kedua makan bilangan 289 terletak antara 100 dan 400. Itu artinya bilangan tersebut akan memberikan hasil puluhan 1. Langkah berikutnya adalah menentukan satuannya dengan cara melihat satuan 289. Satuan 9 hanya dihasilkan dari 3 kuadrat atau 7 kuadrat. Namun secara logika bilangan 289 lebih dekat ke 400 maka kemungkinan akar pangkat 2 dari 289 adalah 17.
b. Tentukan akar pangkat 2 dari 1225.
Bilangan 1225 berada antara 30 kuadrat dan 40 kuadrat karena itu bisa dipastikan angka puluhannya adalah 3. Dengan angka satuan 5 hanya ada satu kemungkinan angka satuan hasilnya yaitu 5. Jadi aka pangkat 2 dari 1225 adalah 35.
Mudah bukan? Memang awalnya terlihat lebih rumit, tapi dengan berlatih pasti akan lebih mudah. Bagaimana dengan akar pangkat 3? Itu justru lebih mudah! Nantikan postingan selanjutnya
http://pintarmatematika.wordpress.com
Cara yang lazim digunakan biasanya dengan cara yang dinamakan mencabut akar. *jadi kebayang mencabut akar singkong. Susahkan. Ini candaanku sama murid
Cara yang saya ajarkan pada murid untuk menentukan akar pangkat 2 adalah sebagai berikut :
1. Saya minta murid menentukan angka satuan (ingat angka satuan, berarti angka yang paling akhir ya
Langkah ini akan menghasilkan daftar seperti ini :
1^2 = 1 (simbol 1^2 dibaca 1 kuadrat ya, atau 1 pangkat 2 atau 1×1
2^2 = 4
3^2 = 9
4^2 = 6 (ingat satuannya saja ya…)
5^2 = 5
6^2 = 6
7^2 = 9
8^2 = 4
9^2 = 1
(Perhatikan ada hasil yang memberikan nilai satuan yang sama. Hati-hati!)
2. Langkah berikutnya adalah menentukan perpangkatan bilangan puluhan.
10^2 = 100
20^2 = 400
30^2 = 900
40^2 = 1600 dan seterusnya.
Penerapan di soal menentukan akar pangkat 2 dari sebuah bilangan :
a. Tentukan akar pangkat 2 dari 289.
Jika melihat dari langkah kedua makan bilangan 289 terletak antara 100 dan 400. Itu artinya bilangan tersebut akan memberikan hasil puluhan 1. Langkah berikutnya adalah menentukan satuannya dengan cara melihat satuan 289. Satuan 9 hanya dihasilkan dari 3 kuadrat atau 7 kuadrat. Namun secara logika bilangan 289 lebih dekat ke 400 maka kemungkinan akar pangkat 2 dari 289 adalah 17.
b. Tentukan akar pangkat 2 dari 1225.
Bilangan 1225 berada antara 30 kuadrat dan 40 kuadrat karena itu bisa dipastikan angka puluhannya adalah 3. Dengan angka satuan 5 hanya ada satu kemungkinan angka satuan hasilnya yaitu 5. Jadi aka pangkat 2 dari 1225 adalah 35.
Mudah bukan? Memang awalnya terlihat lebih rumit, tapi dengan berlatih pasti akan lebih mudah. Bagaimana dengan akar pangkat 3? Itu justru lebih mudah! Nantikan postingan selanjutnya
http://pintarmatematika.wordpress.com
Cara Mudah Menentukan Akar Pangkat 3
Kalau postingan sebelumnya membahas menentukan akar pangkat 2, maka sekarang kita akan belajar cara menentukan akar pangkat 3.
Penentuan akar pangkat 3 suatu bilangan hampir sama caranya dengan penentuan akar pangkat 2. Bahkan ini lebih mudah karena pada penentuan satuan pada akar bilangan pangkat 2 ada beberapa yang memiliki kesamaan. Misalnya jika bilangan tersebut memiliki angka satuan 4 maka ada dua kemungkinan bilangan akarnya. Mungkin 2 atau 8.
Hal tersebut tidak dijumpai pada penentuan akar pangkat 3. Karena disini hanya ada satu jawaban kemungkinan. Untuk lebih jelasnya, ikuti uraian cara kerja penentuan akar pangkat 3 berikut!
1. Tentukan terlebih dahulu angka satuan pada perpangkatan 3 suatu bilangan.
1^3 = 1
2^3 = 8
3^3 = 7 (ingat ya cuma angka satuannya saja)
4^3 = 4
5^3 = 5
6^3 = 6
7^3 = 3
8^3 = 2
9^3 = 9
Perhatikan angka satuannya. Tak ada yang berulang sama sekali. Itu artinya hanya ada satu kemungkinan.
2. Langkah kedua sama seperti langkah kedua menentukan akar pangkat 2. Buatlah pangkat 3 bilangan puluhannya.
10^3 = 1000
20^3 = 8000
30^3 = 27.000 dan seterusnya
Kini cukup menguasai dua langkah itu saja. Berikut latihannya:
Tentukan akar pangkat 3 dari bilangan 13824. Puluhan bilangan itu pasti terdapat diantara 20 dan 30. Karena satuannya adalah 4 maka bisa dipastikan satuan bilangan tersebut adalah 4. Jadi akar pangkat tiga dari bilangan 13824 adalah 24.
http://pintarmatematika.wordpress.com/
Mengenalkan Konsep Bilangan Pecahan Matematika
Materi bilangan pecahan matematika mulai dikenalkan saat murid duduk di kelas 3 Sekolah Dasar. Mereka mulai dikenalkan dengan konsep pecahan dan makna bilangan pecahan dengan lambang
 bilangannya.
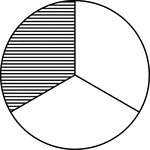
Misalnya pecahan 1/3 ditunjukkan dengan gambar seperti di bawah ini.
Pecahan 1/3 bermakna 1 bagian dari suatu benda utuh yang sebelumnya
telah di’potong’ 3.
bilangannya.
Misalnya pecahan 1/3 ditunjukkan dengan gambar seperti di bawah ini.
Pecahan 1/3 bermakna 1 bagian dari suatu benda utuh yang sebelumnya
telah di’potong’ 3.Sebagai orangtua, Anda pun dapat berperan mengenalkan konsep bilangan pecahan. Gunakan pendekatan yang berbeda dengan cara di sekolah. Di sekolah, pendekatan yang dilakukan biasanya hanya sekadar menunjukkan gambar seperti contoh gambar tadi.
Ada baiknya untuk memberikan benda kongkrit yang menggambarkan pecahan tersebut. Tanpa itu, biasanya akan lebih sulit untuk anak memahami maksud dari bilangan pecahan. Misalnya situasi saat memotong kue menjadi 4 bagian, Anda pun bisa memperkenalkan konsep bilangan pecahan perempatan. Dan mintalah anak untuk menunjukkan bilangan 1/4, 2/4 dan 3/4.
Bahkan konsep bilangan senilai/ setara juga dapat dilakukan dengan pendekatan ini. Anda bisa menunjukkan bahwa bilangan 1/2 itu ternyata memiliki bentuk yang sama besar dengan potongan yang menunjukkan bilangan 2/4 atau 3/6.
Benda lain yang mudah digunakan adalah pita atau tali. Benda ini bahkan lebih memudahkan anak bereksperimen dan memahami dengan baik konsep bilangan pecahan matematika. Bahkan konsep lebih besar atau lebih kecil dengan simbol < dan > dapat terlihat lebih jelas dengan alat peraga ini. Anak tinggal menempelkan dua pita yang hendak disebandingkan.
Selamat bermain sekaligus mengenalkan bilangan pecahan matematika
http://pintarmatematika.wordpress.com/
Bermain Matematika dengan Ular Tangga
Masa seperti sekarang ini, saat ulangan berakhir, biasanya saya mengisi materi di kelas dengan bermain matematika. Maksudnya jelas, anak tetap belajar tapi dalam suasana santai dan menyenangkan. Tahu sendiri kan, kalau tidak dalam format bermain mereka biasanya akan protes dan ogah belajar.
Pada pertemuan sebelumnya saya sudah memberikan permainan matematika dot do dot dan meminta mereka mewarnainya. Dot to dot pun disesuaikan dengan tingkat kesulitan kelas. Misalnya untuk kelas rendah, hanya membilang urut. Sedangkan untuk kelas yang lebih tinggi, biasanya akan saya sajikan dot do dot bilangan genap, bilangan ganjil atau bilangan loncat tertentu. Bisa juga berupa bilangan prima.
Sebagai pengajar, saya memang harus kreatif. Putar otak, akhirnya ketemu format bermain matematika ala ular tangga. Ya betul, ide sebenarnya dari permainan ular tangga yang biasa dimainkan anak-anak. Hanya kali ini, mereka harus menyelesaikan beberapa soal yang berhubungan dengan matematika.
 Sebagaimana
permainan dot to dot, saya pun menyesuaikannya dengan tingkatan kelas.
Berikut adalah contoh bermain matematika dengan ular tangga untuk
tingkatan kelas 2 SD.
Sebagaimana
permainan dot to dot, saya pun menyesuaikannya dengan tingkatan kelas.
Berikut adalah contoh bermain matematika dengan ular tangga untuk
tingkatan kelas 2 SD.Seru kan? Selamat mencoba!
http://pintarmatematika.wordpress.com
Cepat Hafal Perkalian Dasar
Cepat hafal perkalian dasar adalah salah satu kunci keberhasilan belajar matematika di tingkat sekolah dasar. Kurikulum pengajaran matematika di kelas 2 mulai mengenal makna perkalian sebagai penjumlahan yang berulang. Murid biasanya akan dikenalkan konsep perkalian bahwa 2 x 3 itu bermakna 3 + 3 dan bukan 2 + 2 + 2 walaupun keduanya memberikan hasil akhir yang sama.
Sejalan dengan pemahaman murid pada konsep perkalian, alangkah baiknya jika murid juga menghafal perkalian dasar tersebut. Menghafalkan perkalian dasar memudahkan mereka untuk mengerjakan soal-soal yang diberikan baik dalam materi bilangan maupun dalam materi lainnya. Selain itu menghafal perkalian dasar memudahkan murid ketika harus berhadapan dengan perkalian yang lebih kompleks.
Namun tak bisa dipungkiri banyak sekali murid yang tidak menghafal perkalian dasar. Penyebabnya biasanya karena ‘malas’ atau tidak merasa membutuhkan. Untuk menghadapi hal seperti ini, sebagai guru, saya selalu memberi target mereka untuk menghafalkan perkalian dasar secara perlahan. Setiap kali mereka datang, satu persatu murid harus ‘setor’ hafalan mereka. Saya akan menanyakan satu per satu. Jika sudah hafal perkalian 2, maka di pertemua selanjutnya mereka harus menyetor perkalian 3. Begitu seterusnya. Lama kelamaan. masing-masing murid akan hafal perkalian dasar.
Untuk memancing suasana, saya pun kadang membuat suasana lomba hafalan perkalian. Modelnya seperti cerdas cermat gitu. Masing-masing murid akan diberi sejumlah pertanyaan yang berhubungan dengan perkalian dasar. Selain itu adapula pertanyaan rebutan. Biasanya murid akan antusias mengikuti dan termotivasi untuk hafal perkalian dasar.
Jika peserta banyak, saya biasa membaginya dalam beberapa kelompok. Setiap juara kelompok akan diadu kembali untuk mendapatkan pemenang akhir. Tentu saja, saya pun tak lupa menyediakan hadiah-hadiah kecil sebagai penambah semangat. Biasanya berupa permen, penganan kecil, alat tulis, gantungan kunci maupun benda-benda lainnya. Yang penting murah dan meriah.
http://pintarmatematika.wordpress.com
Sistem Bilangan Romawi
Salah satu konsep matematika yang harus dikuasai seorang anak SD adalah bilangan romawi. Berdasarkan pengalaman selama ini, saya selalu melihat ada saja anak yang mengalami kerepotan ketika harus berurusan dengan huruf-huruf yang melambangkan bilangan ini. Padahal ada cara mudah yang dapat dilakukan, yaitu dengan memahami aturan dasar yang berlaku di bilangan romawi.
Untuk mengajarkan seorang anak tentang bilangan romawi, mintalah dia untuk terlebih dahulu mengingat 7 huruf yang melambangkannya. Ketujuh huruf tersebut adalah :
I = 1
V = 5
X = 10
L = 50
C = 100
D = 500
M = 1000
Adapun aturan dasarnya seperti ini :
1. Pengulangan hanya bisa dilakukan pada bilangan 1, 10, 100 dan 1000 (minta anak memperhatikan pola yang terlihat). Jadi tak ada pengulangan untuk 5, 50 dan 500.
Contoh : II = 2 atau CCC = 300
Tapi tidak boleh VV untuk menyatakan 10 (10 dilambangkan dengan X).
2. Pengulangan hanya bisa dilakukan paling banyak tiga kali.
Contoh : III = 3 dan MMM = 3000.
3. Jika lambang bilangan yang lebih kecil berada di depan berarti kurang. Dan jika berada di belakang lambang bilangan yang lebih besar berarti tambah.
Contoh : IV= 4 karena 5 – 1 (minta anak memperhatikan bahwa 4 tidak ditulis sebagai IIII seperti yang ditegaskan aturan kedua)
VIII = 8 karena 5+3
4. Aturan nomor 3 hanya berlaku bagi lambang bilangan yang berdekatan atau selang 1.
Contoh : XL = 40 karena 50-10
XC = 90 karena 100-10
Tapi tak bisa XD melambangkan 490 (500-10) karena penulisan yang tepat untuk 490 adalah CDXC (CD = 400 dan XC=90).
5. Untuk bilangan lebih dari 5000 terjadi pengulangan dengan menambah garis pada bagian atas lambang bilangan romawi tersebut. Contoh 5000 = V (dengan tambahan satu garis di atas V)
Penambahan garis menandakan bahwa bilangan dimaksud dikali 1000.
Setelah itu hendaknya orangtua atau pengajar memberikan banyak contoh soal dan soal-soal untuk memperlancar anak. Berikan soal bolak-balik, yaitu mengubah bentuk sistem bilangan romawi menjadi bentuk arab-hindu yang lazim digunakan dan lakukan hal sebaliknya.
http://pintarmatematika.wordpress.com
MATEMATIKA DAN CARA MENGAJARKANNYA
Jika
merunut catatan sejarah, Matematika telah lahir sejak 3000 SM yaitu
pada saat Bangsa Mesir Kuno dan Babilonia mulai menggunakan aritmetika,
aljabar, dan geometri untuk keperluan astronomi, bangunan dan
konstruksi, perpajakan dan urusan keuangan lainnya. Sistematisasi
matematika menjadi suatu ilmu, baru terjadi pada zaman Yunani Kuno yakni
antara tahun 600 dan 300 SM. Sejak saat itu matematika mulai
berkembang luas, interaksi matematika dengan bidang lain seperti sains
dan teknologi semakin nampak. Kini, matematika telah menjadi alat
penting dalam berbagai hal. Hampir setiap bidang ilmu dan teknologi
memakai matematika. Dalam realita yang demikian, penguasaan terhadap
matematika menjadi syarat perlu agar dapat mempertahankan eksistensi di
era perkembangan ilmu dan teknologi sekarang ini.
Pembelajaran matematika secara formal umumnya diawali di bangku sekolah. Sementara itu, matematika di sekolah masih menjadi pelajaran yang menakutkan bagi para siswa. Di antara berbagai faktor yang memicu hal ini adalah proses pembelajaran yang kurang asyik dan menarik. Model pembelajaran yang sering di temui pada pembelajaran matematika adalah proses pembelajaran bercorak “teacher centered”, yaitu pembelajaran yang berpusat pada guru. Sehingga guru menjadi pemeran utama dan kehadirannya menjadi sangat menentukan. Pembelajaran menjadi tak dapat dilakukan tanpa kehadiran guru. Siswa cenderung pasif dan tidak berperan selama proses pembelajaran. Sehingga proses yang muncul adalah “take and give”. Dalam merangkai pembelajaran, guru pada umumnya terbiasa dengan model standar, yakni pembelajaran yang bermula dari rumus, menghapalnya, kemudian diterapkan dalam contoh soal. Model pembelajaran yang demikian tidak memberi ruang bagi siswa untuk melakukan observasi (mengamati), eksplorasi (menggali), inkuiri (menyelidiki), dan aktivitas-aktivitas lain yang memungkinkan mereka terlibat dan memahami permasalahan yang sesungguhnya. Model seperti ini yang mengakibatkan matematika bak kumpulan rumus yang menyeramkan, sulit dipelajari, dan nampak abstrak. Bagaimana Sebaiknya Matematika Diajarkan?Matematika adalah ilmu realitas, dalam artian ilmu yang bermula dari kehidupan nyata. Selayaknya pembelajarannya dimulai dari sesuatu yang nyata, dari ilustrasi yang dekat dan mampu dijangkau siswa, dan kemudian disederhanakan dalam formulasi matematis. Mengajarkan matematika bukan sekedar menyampaikan aturan-aturan, definisi-definisi, ataupun rumus-rumus yang sudah jadi. Konsep matematika seharusnya disampaikan bermula pada kondisi atau permasalahan nyata. Berikut tahapan pengajaran yang dapat dilakukan:
Sebagai contoh dalam pembelajaran mengenai perbandingan trigonometri . Pembelajaran trigonometri sering kali ditakuti karena yang nampak ke permukaan adalah simbol-simbol dan rumus-rumus yang abstrak. Adapun maknanya jarang diangkat dan dipahamkan kepada para siswa. Perbandingan trigonometri sesungguhnya berawal dari persoalan nyata. Berikut salah satu alternatif pengajaran yang dapat dilakukan:
Proses pembelajaran seperti ini, jika terus dilakukan dan dikembangkan dalam berbagai topik pembelajaran matematika , dimungkinkan akan menciptakan pembelajaran matematika yang lebih asyik dan menarik, sekaligus mengikis pencitraan buruk dan menakutkan yang melekat padanya.
http://www.ubb.ac.id
|
Koset dan Teorema Lagrange
Pengertian koset: jika H adalah subgrup dari grup(G;o) dan adalah elemen
dari G maka Ha = {h o alh∈ H} dapat diartikan sebagai koset kanan dari H
dalam G, sedangkan aH = {a o hlh∈ H} disebut sebagai koset kiri dari H
dalam G.
Teorema Lagrange: jika G adalah suatu grup berhingga dan S adalah subgrup dari G, maka order dari S akan membagi habis order dari G dan dapat dituliskan sebagai n(S)In(G) atau dengan kata lain subgrup akan membagi habis grupnya sehingga dapat ditulis sebagai (S)I(G).
Sebagai contoh:
carilah semua koset dari 4Z ≤ 2Z
di mana Z = {.....-2, -1, 0, 1, 2.......}
maka 2Z = {.....,-4, -2, 0, 2, 4,........} dan 4Z ={......-8, -4, 0, 4, 8............} karena yang akan dicari adalah 4Z ≤ 2Z maka yang akan jadi grup adalah 2Z dan untuk pencarian koset yang digunakan adalah elemen dari 2Z yaitu {........-4 ,-2, 0, 2, 4..........}.
Koset kanan
4Z + 0 = {.......-8, -4, 0, 4, 8........}
4Z + 2 = {.........-6, -2,2,6, 10.......}
4Z + 4 = {........-4, 0, 4, 8..............}
Koset kiri
0 + 4Z = {.......-8, -4, 0, 4, 8........}
2 + 4Z = {.........-6, -2,2,6, 10.......}
4 + 4Z = {........-4, 0, 4, 8..............}
Jadi kosetnya adalah 4Z+ 0, 4Z+2, 0+4Z,2+4Z. Hal ini terjadi karena pada koset 0+4Z dan 4+4Z terjadi pengulangan sehingga dapat dianggap sama, begitu juga pada koset kirinya.
http://www.forumsains.com
Teorema Lagrange: jika G adalah suatu grup berhingga dan S adalah subgrup dari G, maka order dari S akan membagi habis order dari G dan dapat dituliskan sebagai n(S)In(G) atau dengan kata lain subgrup akan membagi habis grupnya sehingga dapat ditulis sebagai (S)I(G).
Sebagai contoh:
carilah semua koset dari 4Z ≤ 2Z
di mana Z = {.....-2, -1, 0, 1, 2.......}
maka 2Z = {.....,-4, -2, 0, 2, 4,........} dan 4Z ={......-8, -4, 0, 4, 8............} karena yang akan dicari adalah 4Z ≤ 2Z maka yang akan jadi grup adalah 2Z dan untuk pencarian koset yang digunakan adalah elemen dari 2Z yaitu {........-4 ,-2, 0, 2, 4..........}.
Koset kanan
4Z + 0 = {.......-8, -4, 0, 4, 8........}
4Z + 2 = {.........-6, -2,2,6, 10.......}
4Z + 4 = {........-4, 0, 4, 8..............}
Koset kiri
0 + 4Z = {.......-8, -4, 0, 4, 8........}
2 + 4Z = {.........-6, -2,2,6, 10.......}
4 + 4Z = {........-4, 0, 4, 8..............}
Jadi kosetnya adalah 4Z+ 0, 4Z+2, 0+4Z,2+4Z. Hal ini terjadi karena pada koset 0+4Z dan 4+4Z terjadi pengulangan sehingga dapat dianggap sama, begitu juga pada koset kirinya.
http://www.forumsains.com
Skala Angka Pengukuran dalam Pandangan Statistik

Skala pengukuran merupakan, satu pengetahuan yang sangat penting sebelum seseorang melakukan pengolahan data. Skala pengukuran pertama kali diperkenalkan oleh S.S. Steven. Namun, sering kali hal ini dianggap remeh dan diabaikan. Pada dasarnya setiap tools (alat bantu hitung) statistik tidak bisa digunakan begitu saja, ada persyaratan (asumsi yang harus dipenuhi), misalnya : skala data, distribusi data, independensi data, dan variabilitas data.
Berdasarkan sifatnya, ada empat pembedaan skala :
1. Skala nominal
Sifat : membedakan.Contoh : jenis kelamin (laki-laki, perempuan), agama (Islam, Katolik, Kristen, Hindu, Budha).
Contoh metode statistik : chi-square, crostab, analisis korespondensi, regresi logistik, latent profile analysis.
2. Skala ordinal
Sifat : membedakan, ada urutan.Contoh : tingkat pendidikan (SD, SMP, SMU, Perguruan tinggi), nilai akreditasi (A, B, C, D, E).
Contoh metode statistik : korelasi spearman, ordinal logistic regression, attribute agreement analysis.
3. Skala interval
Sifat : membedakan, ada urutan, memiliki jarak yang sama.Contoh : usia, skor penilaian test psikologi.
Contoh metode statistik : korelasi pearson, analisis regresi, analisis faktor, K-means cluster, diskriminan.
4. Skala rasio
Sifat : membedakan, ada urutan, memiliki nilai nol mutlak.Contoh : nilai penjualan (sales), jumlah pelanggan.
Contoh metode statistik yang dapat digunakan :korelasi pearson, analisis regresi, analisis faktor, K-means cluster, analisis diskriminan, analisis time series.
http://www.forumsains.com/
Matematika dan Bilangan Prima
Bilangan
prima adalah dasar dari matematika, termasuk salah satu misteri alam
semesta. Tidak pernah terbayangkan oleh manusia sebelumnya, sampai
ditemukan bahwa bilangan prima juga merupakan dasar dari kehidupan alam,
yang dengan usaha keras ingin dijelaskan oleh ilmu ini dalam sains.
Pandangan orang umumnya mengatakan bahwa matematika hanyalah penemuan
manusia biasa. Sebaliknya, beberapa pemikir masa lalu - Pythagoras,
Plato, Cusanus, Kepler, Leibnitz, Newton, Euler, Gauss, termasuk para
revolusioner abad ke-20, Planck, Einstein dan Sommerffeld - yakin bahwa
keberadaan angka dan bentuk geometris merupakan konsep alam semesta dan
konsep yang bebas (independent). Galileo sendiri beranggapan bahwa matematika adalah bahasa Tuhan ketika menulis alam semesta.
Salah satu teka-teki lama yang belum sepenuhnya terpecahkan adalah bilangan prima. Bilangan prima adalah bilangan yang hanya dapat habis dibagi oleh bilangan itu sendiri dan angka 1. Angka 12 bukan merupakan bilangan prima, karena dapat habis dibagi oleh angka lainnya 2, 3, dan 4. Bilangan prima adalah 2, 3, 5, 7, 11, 13, .... dan seterusnya. Banyak bilangan prima tidak terhingga. Tidak peduli berapa banyak kita menghitung, pasti kita akan menemukan bilangan prima, walaupun mungkin makin jarang_ Hal ini menjadi teka-teki kita, jika kita ingat bilangan ini tidak dapat dibagi oleh angka lainnya. Salah satu hal yang menakjubkan, dalam era komputer kita memberikan kodetifikasi semua hal yang penting dan rahasia, di bank, asuransi, dan perhitungan-perhitungan peluru kendali, security system dengan enkripsi, dalam angka jutaan bilangan-bilangan yang tidak habis dibagi oleh angka lainnya. Ini diperlukan karena dengan penggunaan angka lain, kodetifikasi tadi dapat dengan mudah ditembus.
Fenomena inilah yang ditemukan ilmuwan dari Duesseldorf (Dr. Plichta), sehubungan dengan penciptaan alam, yaitu distribusi misterius bilangan prima. Para ilmuwan sudah lama percaya bahwa bilangan prima adalah bahasa universal yang dapat dimengerti oleh semua makhluk (spesies) berintelegensia tinggi, sebagai komunikasi dasar antarmereka. Bahasa ini penuh misteri karena berhubungan dengan perencanaan universal kosmos.
Bilangan lain yang perlu diketahui adalah sisa dari bilangan prima, yakni bilangan komposit, kecuali angka 1, yaitu 4, 6, 8, 9,10,12,14,15, .... dan seterusnya. Dengan kata lain, bilangan komposit adalah bilangan yang terdiri dari minimal dua faktor prima. Misalnya :
6 = 2 x 3 = 2 . 3
30 = 2 x 3 x 5 = 2 . 3 . 5
85 = 5 x 17 = 5 . 17
Selain itu, dikenal pula bilangan khusus, yang disebut prima kembar, yaitu bilangan prima yang angkanya berdekatan dengan selisih 2. Misalnya :
(3,5)
(5,7)
(11,13)
(17,19)
dan seterusnya.
Mayoritas ahli astrofisika juga percaya bahwa di alam semesta terdapat "kode kosmos" atau yang disebut cosmic code based on this order, yang dikenal juga sebagai Theory of Everything (TOE), yang artinya terdapat konstanta-konstanta alam semesta yang saling berhubungan berdasarkan perintah pendesain. Sekali perintah tersebut dapat dipecahkan, maka hal ini akan membuka pandangan sains lainnya yang berhubungan.
Bilangan Prima dan Rencana Penciptaan
Salah satu teka-teki lama yang belum sepenuhnya terpecahkan adalah bilangan prima. Bilangan prima adalah bilangan yang hanya dapat habis dibagi oleh bilangan itu sendiri dan angka 1. Angka 12 bukan merupakan bilangan prima, karena dapat habis dibagi oleh angka lainnya 2, 3, dan 4. Bilangan prima adalah 2, 3, 5, 7, 11, 13, .... dan seterusnya. Banyak bilangan prima tidak terhingga. Tidak peduli berapa banyak kita menghitung, pasti kita akan menemukan bilangan prima, walaupun mungkin makin jarang_ Hal ini menjadi teka-teki kita, jika kita ingat bilangan ini tidak dapat dibagi oleh angka lainnya. Salah satu hal yang menakjubkan, dalam era komputer kita memberikan kodetifikasi semua hal yang penting dan rahasia, di bank, asuransi, dan perhitungan-perhitungan peluru kendali, security system dengan enkripsi, dalam angka jutaan bilangan-bilangan yang tidak habis dibagi oleh angka lainnya. Ini diperlukan karena dengan penggunaan angka lain, kodetifikasi tadi dapat dengan mudah ditembus.
Fenomena inilah yang ditemukan ilmuwan dari Duesseldorf (Dr. Plichta), sehubungan dengan penciptaan alam, yaitu distribusi misterius bilangan prima. Para ilmuwan sudah lama percaya bahwa bilangan prima adalah bahasa universal yang dapat dimengerti oleh semua makhluk (spesies) berintelegensia tinggi, sebagai komunikasi dasar antarmereka. Bahasa ini penuh misteri karena berhubungan dengan perencanaan universal kosmos.
Bilangan lain yang perlu diketahui adalah sisa dari bilangan prima, yakni bilangan komposit, kecuali angka 1, yaitu 4, 6, 8, 9,10,12,14,15, .... dan seterusnya. Dengan kata lain, bilangan komposit adalah bilangan yang terdiri dari minimal dua faktor prima. Misalnya :
6 = 2 x 3 = 2 . 3
30 = 2 x 3 x 5 = 2 . 3 . 5
85 = 5 x 17 = 5 . 17
Selain itu, dikenal pula bilangan khusus, yang disebut prima kembar, yaitu bilangan prima yang angkanya berdekatan dengan selisih 2. Misalnya :
(3,5)
(5,7)
(11,13)
(17,19)
dan seterusnya.
Mayoritas ahli astrofisika juga percaya bahwa di alam semesta terdapat "kode kosmos" atau yang disebut cosmic code based on this order, yang dikenal juga sebagai Theory of Everything (TOE), yang artinya terdapat konstanta-konstanta alam semesta yang saling berhubungan berdasarkan perintah pendesain. Sekali perintah tersebut dapat dipecahkan, maka hal ini akan membuka pandangan sains lainnya yang berhubungan.
http://www.forumsains.com
Menuju Ke Abstrak
Pemahaman akan pengertian abstrak
sepertinya masih dianggap sebagai suatu yang sulit bahkan tak
teraplikasi. Bagi orang di pinggir jalan, boleh jadi menganggap orang
yang belajar matematika abstrak sebagai orang sinting.
Saatnya kita harus menguak apa yang dimaksud abstrak dalam matematika? Apakah suatu yang tidak real? Hanyakah ngoyoworo
ataukah hanyakah khayalan orang? Apakah seperti aljabar abstrak itu
suatu yang mengada-ada saja ataukah memang harus menuju ke situ?
Berikut semoga bisa memberi gambaran akan pemahaman tersebut. Sebagai langkah-langkah sebelum ke abstrak, kita berkecimpung dengan aritmatika yang di dalamnya ada proses seperti penjumlahan, perkalian, dan ada penggunaan variabel. Pengenalan abstrak di SMA biasanya dimulai dengan pelajaran induksi matematik dimana harus membuktikan keteraturan sampai tak hingga dengan membuktikan implikasi Pk--->Pk+1 dan membuktikan P0 benar.
Waktu kita melangkah dari perhitungan dasar ke penggunaan variabel, kita meluaskan orientasi kepada cakupan perhitungan yang lebih luas. Kita bisa mengoperasikan bilangan-bilangan tanpa mengetahui berapa bilangannya, cukup dengan variabel. Nah ini, dari aritmatika menuju abstrak yang banyak membuat kepala para mahasiswa sakit, sebenarnya juga merupakan perluasan orientasi menuju semakin beragam dan semakin luas. Kita mulai dengan mempelajari sekelompok obyek, lalu interaksi antar obyek, yang lalu kita namakan operasi biner, mempelajari keteraturannya, mempelajari ciri-cirinya, lalu memformulasikannya menjadi aksioma-aksioma.
Contoh di bawah mungkin bisa menjadi bayangan akan langkah tersebut, kita mulai dengan PENGANTAR TEORI BILANGAN.
Subgroup bilangan bulat
Kita perhatikan perhatikan himpunan bilangan bulat (integer), yaitu {...,-3,-2,-1,0,1,2,3,...} yang lalu biasa dinotasikan dengan Z. < huruf Z ini adalah diambil dari singkatan Zahl=bilangan dari Bhs Jerman>
Diberikan suatu himpunan bagian dari Z, katakanlah himpunan S. Himpunan S disebut subgroup dari Z jika memenuhi :
(i) x+y anggota dari S untuk setiap x dan y anggota dari S,
(ii) 0 anggota dari S,
(iii) -x anggota dari S untuk setiap x anggota dari S.
Berikut semoga bisa memberi gambaran akan pemahaman tersebut. Sebagai langkah-langkah sebelum ke abstrak, kita berkecimpung dengan aritmatika yang di dalamnya ada proses seperti penjumlahan, perkalian, dan ada penggunaan variabel. Pengenalan abstrak di SMA biasanya dimulai dengan pelajaran induksi matematik dimana harus membuktikan keteraturan sampai tak hingga dengan membuktikan implikasi Pk--->Pk+1 dan membuktikan P0 benar.
Waktu kita melangkah dari perhitungan dasar ke penggunaan variabel, kita meluaskan orientasi kepada cakupan perhitungan yang lebih luas. Kita bisa mengoperasikan bilangan-bilangan tanpa mengetahui berapa bilangannya, cukup dengan variabel. Nah ini, dari aritmatika menuju abstrak yang banyak membuat kepala para mahasiswa sakit, sebenarnya juga merupakan perluasan orientasi menuju semakin beragam dan semakin luas. Kita mulai dengan mempelajari sekelompok obyek, lalu interaksi antar obyek, yang lalu kita namakan operasi biner, mempelajari keteraturannya, mempelajari ciri-cirinya, lalu memformulasikannya menjadi aksioma-aksioma.
Contoh di bawah mungkin bisa menjadi bayangan akan langkah tersebut, kita mulai dengan PENGANTAR TEORI BILANGAN.
Subgroup bilangan bulat
Kita perhatikan perhatikan himpunan bilangan bulat (integer), yaitu {...,-3,-2,-1,0,1,2,3,...} yang lalu biasa dinotasikan dengan Z. < huruf Z ini adalah diambil dari singkatan Zahl=bilangan dari Bhs Jerman>
Diberikan suatu himpunan bagian dari Z, katakanlah himpunan S. Himpunan S disebut subgroup dari Z jika memenuhi :
(i) x+y anggota dari S untuk setiap x dan y anggota dari S,
(ii) 0 anggota dari S,
(iii) -x anggota dari S untuk setiap x anggota dari S.
< catatan : Kalau pernah
mempelajari tentang teori group, maka syarat-syarat di atas tidak lain
sifat tertutup(i), ada elemen identitas(ii), dan untuk setiap anggota
dari S yang bukan 0 punya invers. Di kasus bilangan bulat ini sifat asosiatif bisa dirunut dg mudah dari sifat tertutup >
Suatu himpunan bagian tak kosong S
dari Z adalah subgroup jika dan hanya jika x - y anggota dari S untuk
setiap x dan y anggota dari S.
Bukti :
S subgroup dari Z ==> x - y anggota S untuk setiap x,y anggota S
Karena y anggota dari S, maka -y anggota dari S
Karena x dan -y anggota dari S, maka x+(-y)=x-y anggota dari S
x - y anggota S untuk setiap x,y anggota S ==> S subgroup dari Z
Karena S tak kososng maka ada anggotanya, misalkan x anggota dari S, maka x-x=0 adalah anggota dari S
Bukti :
S subgroup dari Z ==> x - y anggota S untuk setiap x,y anggota S
Karena y anggota dari S, maka -y anggota dari S
Karena x dan -y anggota dari S, maka x+(-y)=x-y anggota dari S
x - y anggota S untuk setiap x,y anggota S ==> S subgroup dari Z
Karena S tak kososng maka ada anggotanya, misalkan x anggota dari S, maka x-x=0 adalah anggota dari S
Taruhlah m adalah bilangan bulat, dan kita buat notasi mZ={mn|n anggota Z}. Maka mZ
Teorema I
Jika S adalah saubgroup dari Z, maka S = mZ untuk suatu bilngan bulat tak negatif m. < dengan kata lain, teorema ini mengatakan bahwa kalau S adalah subgroup dari Z, maka pasti berbentuk himpunan kelipatan dari suatu bilangan bulat tak negatif {0,1,2,3,...} >
Bukti :
Kita buat dua kemungkinan, yaitu :
pertama --> jika S = {0}, maka dapat ditulis S=mZ dengan m=0.
kedua --> jika S tidak sama dengan {0}, atau S memuat bilangan bulat tak nol. Maka tentunya S memuat bilangan bulat positif < karena jika x anggota S maka -x juga anggota S >. Kita ambil misalnya m adalah bilangan bulat positif yang terkecil di S. Lalu suatu bilangan bulat positif n di S akan dapat ditulis dalam bentuk n=qm+r, dimana q adalah suatu bilangan bulat positif dan r suatu bilangan bulat yang memenuhi 0<=r. Dengan demikian r juga anggota S, karena r=n-qm. Karena diasumsikan m adalah yang terkecil, maka haruslah r=0. Jadi n=qm, dengan demikian n anggota mZ, yang berarti S=mZ. Terbukti.
Teorema tersebut mengatakan bahwa kalau sebuah himpunan yang anggotanya bilangan-bilangan bulat serta memenuhi tiga aksioma untuk subgroup di atas, maka tentulah anggota-anggota himpunan tersebut berbentuk kelipatan dari suatu bilangan bulat positif.
Jika S adalah saubgroup dari Z, maka S = mZ untuk suatu bilngan bulat tak negatif m. < dengan kata lain, teorema ini mengatakan bahwa kalau S adalah subgroup dari Z, maka pasti berbentuk himpunan kelipatan dari suatu bilangan bulat tak negatif {0,1,2,3,...} >
Bukti :
Kita buat dua kemungkinan, yaitu :
pertama --> jika S = {0}, maka dapat ditulis S=mZ dengan m=0.
kedua --> jika S tidak sama dengan {0}, atau S memuat bilangan bulat tak nol. Maka tentunya S memuat bilangan bulat positif < karena jika x anggota S maka -x juga anggota S >. Kita ambil misalnya m adalah bilangan bulat positif yang terkecil di S. Lalu suatu bilangan bulat positif n di S akan dapat ditulis dalam bentuk n=qm+r, dimana q adalah suatu bilangan bulat positif dan r suatu bilangan bulat yang memenuhi 0<=r. Dengan demikian r juga anggota S, karena r=n-qm. Karena diasumsikan m adalah yang terkecil, maka haruslah r=0. Jadi n=qm, dengan demikian n anggota mZ, yang berarti S=mZ. Terbukti.
Teorema tersebut mengatakan bahwa kalau sebuah himpunan yang anggotanya bilangan-bilangan bulat serta memenuhi tiga aksioma untuk subgroup di atas, maka tentulah anggota-anggota himpunan tersebut berbentuk kelipatan dari suatu bilangan bulat positif.
Faktor Persekutuan Terbesar
Definisi :
Taruhlah a1,a2,...,ar adalah bilangan bulat, yang tidak semuanya nol. Faktor persekutuan dari a1,a2,...,ar adalah suatu bilangan bulat yang membagi habis setiap a1,a2,...,ar. Faktor persekutuan terbesar dari a1,a2,...,ar adalah bilangan bulat positif terbesar yang membagi habis setiap a1,a2,...,ar. Faktor persekutuan terbesar dari a1,a2,...,ar dinaotasikan dengan (a1,a2,...,ar).
Definisi :
Taruhlah a1,a2,...,ar adalah bilangan bulat, yang tidak semuanya nol. Faktor persekutuan dari a1,a2,...,ar adalah suatu bilangan bulat yang membagi habis setiap a1,a2,...,ar. Faktor persekutuan terbesar dari a1,a2,...,ar adalah bilangan bulat positif terbesar yang membagi habis setiap a1,a2,...,ar. Faktor persekutuan terbesar dari a1,a2,...,ar dinaotasikan dengan (a1,a2,...,ar).
Teorema II
Taruhlah a1,a2,...,ar adalah bilangan bulat, yang tidak semuanya nol. Maka ada bilangan-bilangan bulat sebutlah u1,u2,...,ur sedemikian hingga
(a1,a2,...,ar)=a1u1 + a2u2 + . . . +arur
dimana (a1,a2,...,ar) adalah Faktor Persekutuan Terbesar dari a1,a2,...,ar.
Bukti :
Pembuktian teorema ini, pertama kita harus menunjukkan bahwa suatu himpunan S yang anggota-anggotanya berbentuk n1a1 + n2a2 + . . . +nrar dimana n1, n2,..., nr bilangan-bilangan bulat merupakan subgroup dari Z dengan menunjukkan terpenuhinya 3 aksioma di atas. Lalu setelah terbukti, maka karena
S subgroup Z, akan berbentuk mZ. Dengan kata lain bahwa setiap anggota S merupakan kelipatan dari m. Dengan demikian m adalah faktor persekutuan dari a1,a2,...,ar. Karena FPB adalah faktor persekutuan, maka otomatis ada u1,u2,...,ur sehingga (a1,a2,...,ar)=a1u1 + a2u2 + . . . +arur. Terbukti.
Kiranya, ini bisa menjadi gambaran bahwa yang namanya abstrak bukan suatu yang tidak aplikatif, melainkan adalah perluasan orientasi kita dalam memandang. Memang terlihat lebih sulit, karena kita mencoba menengok yang disebalik dari yang nampak.
Semoga bermanfaat bagi semuanya.
Taruhlah a1,a2,...,ar adalah bilangan bulat, yang tidak semuanya nol. Maka ada bilangan-bilangan bulat sebutlah u1,u2,...,ur sedemikian hingga
(a1,a2,...,ar)=a1u1 + a2u2 + . . . +arur
dimana (a1,a2,...,ar) adalah Faktor Persekutuan Terbesar dari a1,a2,...,ar.
Bukti :
Pembuktian teorema ini, pertama kita harus menunjukkan bahwa suatu himpunan S yang anggota-anggotanya berbentuk n1a1 + n2a2 + . . . +nrar dimana n1, n2,..., nr bilangan-bilangan bulat merupakan subgroup dari Z dengan menunjukkan terpenuhinya 3 aksioma di atas. Lalu setelah terbukti, maka karena
S subgroup Z, akan berbentuk mZ. Dengan kata lain bahwa setiap anggota S merupakan kelipatan dari m. Dengan demikian m adalah faktor persekutuan dari a1,a2,...,ar. Karena FPB adalah faktor persekutuan, maka otomatis ada u1,u2,...,ur sehingga (a1,a2,...,ar)=a1u1 + a2u2 + . . . +arur. Terbukti.
Kiranya, ini bisa menjadi gambaran bahwa yang namanya abstrak bukan suatu yang tidak aplikatif, melainkan adalah perluasan orientasi kita dalam memandang. Memang terlihat lebih sulit, karena kita mencoba menengok yang disebalik dari yang nampak.
Semoga bermanfaat bagi semuanya.
http://www.forumsains.com
Misteri Bilangan Lubang Hitam : 123
Dalam astronomi dan fisika, kita mengenal adanya suatu fenomena alam yang sangat menarik yaitu lubang hitam (black hole). Lubang hitam adalah suatu entitas yang memiliki medan
gravitasi yang sangat kuat sehingga setiap benda yang telah jatuh di
wilayah horizon peristiwa (daerah di sekitar inti lubang hitam), tidak
akan bisa kabur lagi. Bahkan radiasi elektromagnetik seperti cahaya pun
tidak dapat melarikan diri, akibatnya lubang hitam menjadi "tidak
kelihatan".
Ternyata, dalam matematika juga ada fenomena unik yang mirip dengan fenomena lubang hitam yaitu bilangan lubang hitam. Bagaimana sebenarnya bilangan lubang hitam itu? Mari kita bermain-main sebentar dengan angka.
Coba pilih
sesuka hati Anda sebuah bilangan asli (bilangan mulai dari 1 sampai tak
hingga). Sebagai contoh, katakanlah 141.985. Kemudian hitunglah jumlah
digit genap, digit ganjil, dan total digit bilangan tersebut. Dalam
kasus ini, kita dapatkan 2 (dua buah digit genap), 4 (empat buah digit
ganjil), dan 6 (enam adalah jumlah total digit). Lalu gunakan
digit-digit ini (2, 4, dan 6) untuk membentuk bilangan berikutnya, yaitu
246.
Ulangi
hitung jumlah digit genap, digit ganjil, dan total digit pada bilangan
246 ini. Kita dapatkan 3 (digit genap), 0 (digit ganjil), dan 3 (jumlah
total digit), sehingga kita peroleh 303. Ulangi lagi hitung jumlah digit
genap, ganjil, dan total digit pada bilangan 303. (Catatan: 0 adalah
bilangan genap). Kita dapatkan 1, 2, 3 yang dapat dituliskan 123.
Jika kita mengulangi langkah di atas terhadap bilangan 123, kita akan dapatkan 123 lagi. Dengan demikian, bilangan 123
melalui proses ini adalah lubang hitam bagi seluruh bilangan lainnya.
Semua bilangan di alam semesta akan ditarik menjadi bilangan 123 melalui
proses ini, tak satu pun yang akan lolos.
Tapi
benarkah semua bilangan akan menjadi 123? Sekarang mari kita coba suatu
bilangan yang bernilai sangat besar, sebagai contoh katakanlah
122333444455555666666777777788888888999999999. Jumlah digit genap,
ganjil, dan total adalah 20, 25, dan 45. Jadi, bilangan berikutnya
adalah 202.545. Lakukan lagi iterasi (pengulangan), kita peroleh 4, 2,
dan 6; jadi sekarang kita peroleh 426. Iterasi sekali lagi terhadap 426
akan menghasilkan 303 dan iterasi terakhir dari 303 akan diperoleh 123.
Sampai pada titik ini, iterasi berapa kali pun terhadap 123 akan tetap
diperoleh 123 lagi. Dengan demikian, 123 adalah titik absolut sang
lubang hitam dalam dunia bilangan.
Namun,
apakah mungkin saja ada suatu bilangan, terselip di antara rimba raya
alam semesta bilangan yang jumlahnya tak terhingga ini, yang dapat lolos
dari jeratan maut sang bilangan lubang hitam, sang 123 yang misterius
ini?
http://www.forumsains.com
Misteri Bilangan Nol
Ratusan tahun
yang lalu, manusia hanya mengenal 9 lambang bilangan yakni 1, 2, 2, 3,
5, 6, 7, 8, dan 9. Kemudian, datang angka 0, sehingga jumlah lambang
bilangan menjadi 10 buah. Tidak diketahui siapa pencipta bilangan 0,
bukti sejarah hanya memperlihatkan bahwa bilangan 0 ditemukan pertama
kali dalam zaman Mesir kuno. Waktu itu bilangan nol hanya sebagai
lambang. Dalam zaman modern, angka nol digunakan tidak saja sebagai
lambang, tetapi juga sebagai bilangan yang turut serta dalam operasi
matematika. Kini, penggunaan bilangan nol telah menyusup jauh ke dalam
sendi kehidupan manusia. Sistem berhitung tidak mungkin lagi mengabaikan
kehadiran bilangan nol, sekalipun bilangan nol itu membuat kekacauan
logika. Mari kita lihat.
Nol, penyebab komputer macet
Pelajaran
tentang bilangan nol, dari sejak zaman dahulu sampai sekarang selalu
menimbulkan kebingungan bagi para pelajar dan mahasiswa, bahkan
masyarakat pengguna. Mengapa? Bukankah bilangan nol itu mewakili sesuatu
yang tidak ada dan yang tidak ada itu ada, yakni nol. Siapa yang tidak
bingung? Tiap kali bilangan nol muncul dalam pelajaran Matematika selalu
ada ide yang aneh. Seperti ide jika sesuatu yang ada dikalikan dengan 0
maka menjadi tidak ada. Mungkinkah 5*0 menjadi tidak ada? (* adalah
perkalian). Ide ini membuat orang frustrasi. Apakah nol ahli sulap?
Lebih parah
lagi-tentu menambah bingung-mengapa 5+0=5 dan 5*0=5 juga? Memang
demikian aturannya, karena nol dalam perkalian merupakan bilangan
identitas yang sama dengan 1. Jadi 5*0=5*1. Tetapi, benar juga bahwa
5*0=0. Waw. Bagaimana dengan 5o=1, tetapi 50o=1
juga? Ya, sudahlah. Aturan lain tentang nol yang juga misterius adalah
bahwa suatu bilangan jika dibagi nol tidak didefinisikan. Maksudnya,
bilangan berapa pun yang tidak bisa dibagi dengan nol. Komputer yang
canggih bagaimana pun akan mati mendadak jika tiba-tiba bertemu dengan
pembagi angka nol. Komputer memang diperintahkan berhenti berpikir jika
bertemu sang divisor nol.
Bilangan nol: tunawisma
Bilangan
disusun berdasarkan hierarki menurut satu garis lurus. Pada titik awal
adalah bilangan nol, kemudian bilangan 1, 2, dan seterusnya. Bilangan
yang lebih besar di sebelah kanan dan bilangan yang lebih kecil di
sebelah kiri. Semakin jauh ke kanan akan semakin besar bilangan itu.
Berdasarkan derajat hierarki (dan birokrasi bilangan), seseorang jika
berjalan dari titik 0 terus-menerus menuju angka yang lebih besar ke
kanan akan sampai pada bilangan yang tidak terhingga. Tetapi, mungkin
juga orang itu sampai pada titik 0 kembali. Bukankah dunia ini bulat?
Mungkinkah? Bukankah Columbus mengatakan bahwa kalau ia berlayar
terus-menerus ia akan sampai kembali ke Eropa?
Lain lagi. Jika
seseorang berangkat dari nol, ia tidak mungkin sampai ke bilangan 4
tanpa melewati terlebih dahulu bilangan 1, 2, dan 3. Tetapi, yang lebih
aneh adalah pertanyaan mungkinkan seseorang bisa berangkat dari titik
nol? Jelas tidak bisa, karena bukankah titik nol sesuatu titik yang
tidak ada? Aneh dan sulit dipercaya? Mari kita lihat lebih jauh.
Jika di antara
dua bilangan atau antara dua buah titik terdapat sebuah ruas. Setiap
bilangan mempunyai sebuah ruas. Jika ruas ini dipotong-potong kemudian
titik lingkaran hitam dipindahkan ke tengah-tengah ruas, ternyata
bilangan 0 tidak mempunyai ruas. Jadi, bilangan nol berada di
awang-awang. Bilangan nol tidak mempunyai tempat tinggal alias
tunawisma. Itulah sebabnya, mengapa bilangan nol harus menempel pada
bilangan lain, misalnya, pada angka 1 membentuk bilangan 10, 100, 109,
10.403 dan sebagainya. Jadi, seseorang tidak pernah bisa berangkat dari
angka nol menuju angka 4. Kita harus berangkat dari angka 1.
Mudah, tetapi salah
Guru meminta
Ani menggambarkan sebuah garis geometrik dari persamaan 3x+7y = 25. Ani
berpikir bahwa untuk mendapatkan garis itu diperlukan dua buah titik
dari ujung ke ujung. Tetapi, setelah berhitung-hitung, ternyata cuma ada
satu titik yang dilewati garis itu, yakni titik A(6, 1), untuk x=6 dan
y=1. Sehingga Ani tidak bisa membuat garis itu. Sang guru mengingatkan
supaya menggunakan bilangan nol. Ya, itulah jalan keluarnya. Pertama,
berikan y=0 diperoleh x=(25-0)/3=8 (dibulatkan), merupakan titik
pertama, B(8,0). Selanjutnya berikan x=0 diperoleh y=(25-3.0)/7=4
(dibulatkan), merupakan titik kedua C(0,4). Garis BC, adalah garis yang
dicari. Namun, betapa kecewanya sang guru, karena garis itu tidak
melalui titik A. Jadi, garis BC itu salah.
Ani membela
diri bahwa kesalahan itu sangat kecil dan bisa diabaikan. Guru
menyatakan bahwa bukan kecil besarnya kesalahan, tetapi manakah yang
benar? Bukankah garis BC itu dapat dibuat melalui titik A? Kata guru,
gunakan bilangan nol dengan cara yang benar. Bagaimana kita harus
membantu Ani membuat garis yang benar itu? Mudah, kata konsultan
Matematika. Mula-mula nilai 25 dalam 3x+7y harus diganti dengan hasil
perkalian 3 dan 7 sehingga diperoleh 3x+7y=21.
Selanjutnya,
dalam persamaan yang baru, berikan y=0 diperoleh x=21/3=7 (tanpa
pembulatan) itulah titik pertama P(6,1). Kemudian berikan nilai x=0
diperoleh y=21/7 = 3 (tanpa pembulatan), itulah titik kedua Q(0, 3).
Garis PQ adalah garis yang sejajar dengan garis yang dicari, yakni
3x+7y=25. Melalui titik A tarik garis sejajar dengan PQ diperoleh garis
P1Q1. Nah, begitulah. Sang murid telah menemukan garis yang benar berkat
bantuan bilangan nol.
Akan tetapi,
sang guru masih sangat kecewa karena sebenarnya tidak ada satu garis pun
yang benar. Bukankah dalam persamaan 3x1+7x2=25 hanya ada satu titik
penyelesaian yakni titik A, yang berarti persamaan 3x1+7x2 itu hanya
berbentuk sebuah titik? Bahkan pada persamaan 3x1+7x2=21 tidak ada
sebuah titik pun yang berada dalam garis PQ. Oleh karena itu, garis PQ
dalam sistem bilangan bulat, sebenarnya tidak ada. Aneh, bilangan nol
telah menipu kita. Begitulah kenyataannya, sebuah persamaan tidak selalu
berbentuk sebuah garis.
Bergerak, tetapi diam
Bilangan tidak
hanya terdiri atas bilangan bulat, tetapi juga ada bilangan desimal
antara lain dari 0,1; 0,01; 0,001; dan seterusnya sekuat-kuat kita bisa
menyebutnya sampai sedemikian kecilnya. Karena sangat kecil tidak bisa
lagi disebut atau tidak terhingga dan pada akhirnya dianggap nol saja.
Tetapi, ide ini ternyata sempat membingungkan karena jika bilangan tidak
terhingga kecilnya dianggap nol maka berarti nol adalah bilangan
terkecil? Padahal, nol mewakili sesuatu yang tidak ada? Waw. Begitulah.
Berdasarkan
konsep bilangan desimal dan kontinu, maka garis bilangan yang kita pakai
ternyata tidak sesederhana itu karena antara dua bilangan selalu ada
bilangan ke tiga. Jika seseorang melompat dari bilangan 1 ke bilangan 2,
tetapi dengan syarat harus melompati terlebih dahulu ke bilangan
desimal yang terdekat, bisakah? Berapakah bilangan desimal terdekat
sebelum sampai ke bilangan 2? Bisa saja angka 1/2. Tetapi, anda tidak
boleh melompati ke angka 1/2 karena masih ada bilangan yang lebih kecil,
yakni 1/4. Seterusnya selalu ada bilangan yang lebih dekat... yakni 0,1
lalu ada 0,01, 0,001, ..., 0,000001. demikian seterusnya, sehingga pada
akhirnya bilangan yang paling dekat dengan angka 1 adalah bilangan yang
demikian kecilnya sehingga dianggap saja nol. Karena bilangan terdekat
adalah nol alias tidak ada, maka Anda tidak pernah bisa melompat ke
bilangan 2?
http://www.forumsains.com
Langganan:
Komentar (Atom)